简单易懂的魔方颜色组合的计算方法

选择字号： 超大 标准 发布时间：2016年10月21日 | 作者：imofang | 0个评论 | 65484人浏览

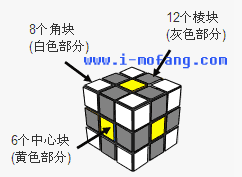
首先，一个三阶魔方一共有几个方块呢？魔方共有三层，一层是9个，3×9=27，但是中间层的中央方块不可见，要排除在外，所以共有26个方块。

这些方块可以分为三类，角块、棱块和中心块，如图所示：

下面，我们就来计算一下这26个方块可能形成的组合数究竟有多少。

1、先看角块可能的组合

假设魔方的八个顶角是八个箱子，我们把角块从1到8编号，现在要这八个角块放到箱子里，那么，

第一个箱子可以从8个角块中任意取一个放进去；

第二个箱子可以从剩余的7个角块中任意取一个放进去；

。。。

第八个箱子没得选择，只能把剩余的一个放进去。

所以，角块可能的组合共有8×7×6×5×4×3×2×1=8! 种。

2、再看棱块可能的组合

类似地，假设魔方的十二个棱块是十二个箱子，我们把棱块从1到12编号，现在要把十二个棱块放到箱子里，那么，

棱块可能的组合共12×11×10×9×8×7×6×5×4×3×2×1=12! 种。

3、角块和棱块颜色的组合

根据上面1和2的结果，可以得出，魔方可能的组合数=8!×12! 种，但是且慢，我们好像没有考虑到块的朝向。

（1）对每个角块来说，它有三种朝向，朝向改变的时候，组合数相应会变化，共有八个角块，所以，朝向的组合有3×3×3×3×3×3×3×3=3^8；

（2）对每个棱块来说，它有两种朝向，朝向改变的时候，组合数相应会变化，共十二个棱块，所以，朝向的组合有2×2×2×2×2×2×2×2×2×2×2×2=2^12；

那么，26个方块可能的组合就是：（8!×3⁸）×（12!×2¹²） 种。

同时，因为魔方本身转动的限制，必须考虑下面三点：

（1）7个角块装好之后，第8个角块只有一个方向，而不是三个，所以要除以3。比如下面的魔方，只有图1的情况是正确的，其它情况下魔方不可能还原，因而是不可能存在的。

（2）11个棱块装好之后，第12个棱块的方向只有一个，而不是二个，所以要除以2；

（3）一旦装好10个棱块之后，第11、12个棱的位置不能互换，是固定死的所以要除以2。

那么，最后总组合数就是：

(8!×3⁸)(12!×2¹²)/(3×2×2)=43252003274489856000，约等于4325亿亿种组合。

（可能有读者注意到这里的计算没有考虑六个中心块。实际上，中心块是无需考虑的，原因是无论角块和棱块的位置如何变化，六个中心块的相对位置是固定不变的。）

除特别注明外，本站所有文章均为爱魔方原创(学魔方请联系微信:18076554217)，原创不易，转载请联系作者授权并注明作者和出处来自http://i-mofang.com/i/?id=51

标签：魔方知识

猜你喜欢