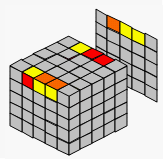
2. 合并好棱块
[1]目标：合并好棱块
| 完成前 | 完成后 | |
 |
→ |  |
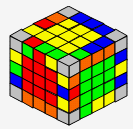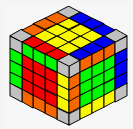[2]转动窍门：
这一步是把同色、但不在同一边上的3个棱块拼到一起，一共是36个棱块，要组成12条的同色同边的棱块。
拼棱块对的方法，简单地说：
(1) 任意找一个棱块，找到同色的另一个棱块，把这2个棱块拼到一起
(2) 拼到一起的2个棱块移到旁边，并用杂乱(没拼好)的棱块代替
(3) 恢复弄乱的的中心块
(4) 找到同色的第3个棱块，让刚才拼到一起的2个棱块和第3个棱块拼到一起
(5) 拼到一起的3个棱块移到旁边，并用杂乱的棱块代替
(6) 恢复弄乱的的中心块
用相同的方法把余下的棱块拼好，具体的转动方法请看下面[3]的【情况1】的详细图解。
另外，在拼棱的过程中，可能会碰到如下的3种情况,点击图像会跳到相应的解法。
| 情况2 (剩下3个边未对好) |
情况3 (剩下2个边未对好) |
情况4 (剩下1个边未对好) |
 |
 |
 |
[3]详细图解：
情况1：拼棱的方法(下图以绿白棱为例说明)
 |
→ |  |
→ |  |
|
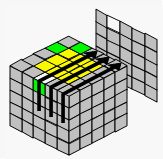| 找到一个同色的棱块 | 把该棱块移到对面 | 拼成一对 | |||
| → |  |
→ |  |
→ |  |
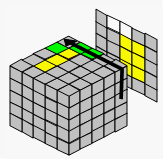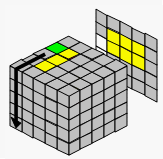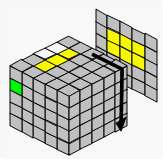| 移到旁边 | 用杂乱的棱块代替 | 准备恢复中心块 | |||
| → |  |
→ |  |
→ |  |
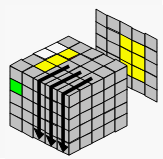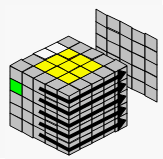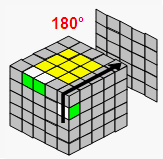| 恢复中心块 | 为说明方便，整体转动一下 | 找到第3个棱块 | |||
| → |  |
→ |  |
→ |  |
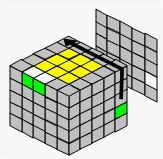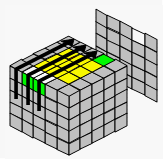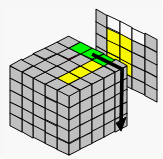| 把该棱块移到对面 | 把3个棱块拼到一起 | 移动 | |||
| → |  |
→ |  |
→ |  |
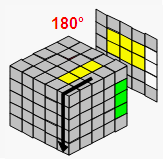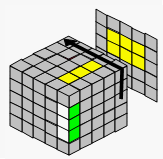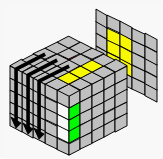| 移到一边 | 用杂乱的棱块代替 | 恢复中心块 | |||
| → |  |
||||
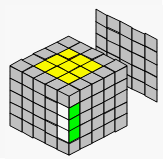| 拼好了3个绿色棱块 |
情况2：只剩3边未对好
| 1)判断剩余的3边是否可以拼好棱，前提： ① 其中两边已经转到相对的位置，并且转动一次能对好3个块(如图中A方向的蓝白块) ② 第三边已经转到前两边的侧面位置(如图中B方向的边) |
|||||
 |
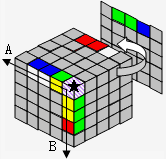→ 最顶层向右转90度 |
 |
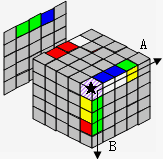→ 为了好说明，整体向左转90度 |
 |
|
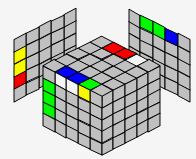| 以★号为原点，因为 A方向的块:1单2双 B方向的块:2双1单 ,所以，不能拼好棱 |
以★号为原点，因为 A方向的块:2双1单 B方向的块:2双1单 ,所以，可以拼好棱 |
经如此变换之后，就可以按照下面的（拼好3边）的说明，一次即拼好3边 | |||
2)拼好3边 |
|||||
 |
→ |  |
→ |  |
|
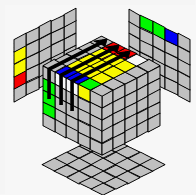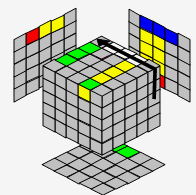| 准备拼好蓝白3个棱块 | 已拼好,移到旁边 | L' | |||
| → |  |
→ |  |
→ |  |
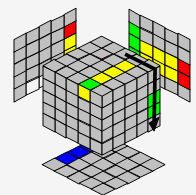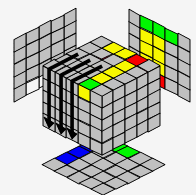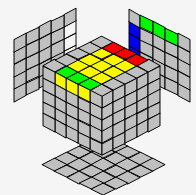| 用第3个没拼好的边代替 | 恢复中心块 | ||||
情况3：只剩2边未对好(例:绿白、蓝黄)，做5次(TR U2)就会变为情况2(即剩下3边没对好)
 |
 |
→ |  |
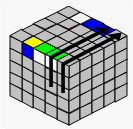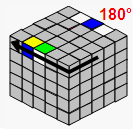→ | TR U2做5次后会变为情况2 | ||
| TR | U2 |
情况4-1：只剩1边未对好（用公式解）
 |
→ |  |
→ |  |
→ |  |
|
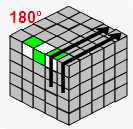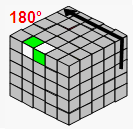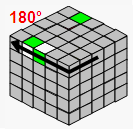| TR2 | B2 | U2 | TL | ||||
| → |  |
→ |  |
→ |  |
→ |  |
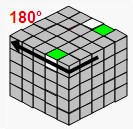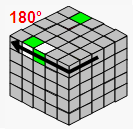| U2 | TR' | U2 | TR | ||||
| → |  |
→ |  |
→ |  |
→ |  |
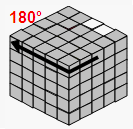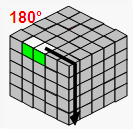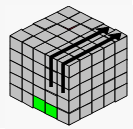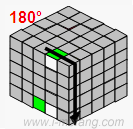| U2 | F2 | TR | F2 | ||||
| → |  |
→ |  |
→ |  |
→ |  |
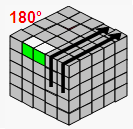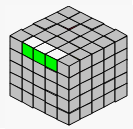| TL' | B2 | TR2 |
情况4-2：只剩1边未对好（如果觉得上面的公式法难记忆，可以通过理解法，把拼好的棱拆分开）
 |
→ |  |
→ |  |
|
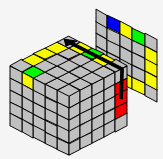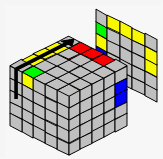| Rt | B | L' | |||
| → |  |
→ |  |
→ |  |
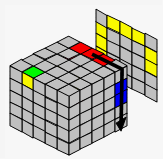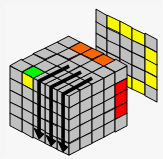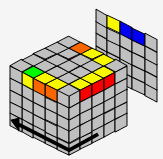| B' | R't | D' | |||
| → |  |
→ |  |
→ |  |
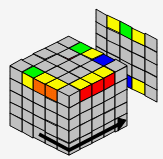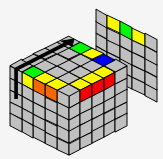| B2 | D | L' | |||
| → |  |
→ |  |
→ |  |
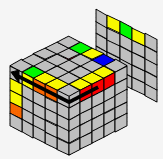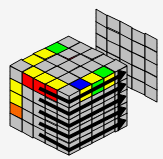| U | y' | TL' | |||
| → |  |
→ |  |
→ |  |
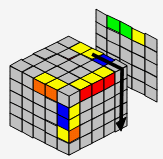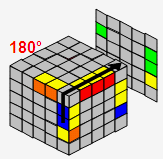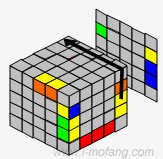| B' | R2 | B | |||
| → |  |
→ |  |
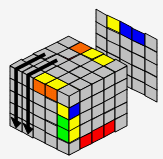→ | 变为只剩2边，按照(情况3)的说明去解即可 |
| TL |
